Einführungsbeispiel Hypothesentests
Die Firma Knopfloch AG stellt Knöpfe her.  Die Ausschussrate beträgt 1%.
Die Ausschussrate beträgt 1%.
Nach einer Modernisierung der Maschinen wird vermutet, dass die Ausschussrate nun auf höchstens 0,5% gesunken ist.
Dies nennt man die Nullhypothese H0.
Wir, die Hemdenträger GmbH, wollen diese Aussage prüfen und fordern eine Stichprobe von 1000 Knöpfen.
In dieser Stichprobe befinden sich 9 schadhafte Knöpfe.
Sollen wir nun aufgrund dieser Daten glauben, dass die Ausschussrate auf höchstens 0,5% abgesunken ist?
Mit anderen Worten: Sollen wir die Nullhypothese H0 annehmen oder doch besser ablehnen?
Zunächst veranschaulichen wir uns die Wahrscheinlichkeitsverteilung in einem Histogramm.
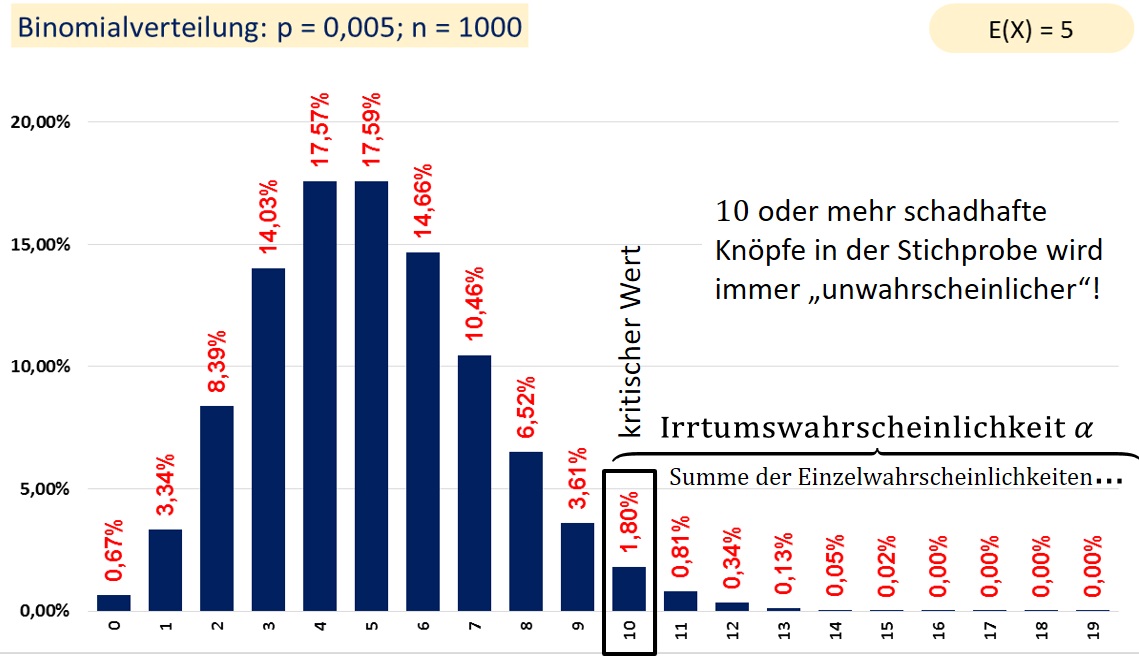
Nun überlegen wir uns, ab wie vielen schadhaften Knöpfen wir die Behauptung (also die Nullhypothese H0) ablehnen wollen.
Dazu legen wir eine kritische Grenze, sagen wir mal 10 schadhafte Knöpfe fest, denn wir sehen am Histogramm, dass 10 schadhafte Knöpfe in der Stichprobe vorzufinden schon sehr unwahrscheinlich ist.
Mit der Vorgabe dieses kritischen Werts legen wir einen Ablehnungsbereich von [10;1000] fest. Das Gegenstück davon [0;9] ist der Annahmebereich. Wenn wir nämlich zwischen 0 und 9 schadhafte Knöpfe in der Stichprobe zählen, glauben wir der Knopfloch AG die Behauptung.
Irrtumswahrscheinlichkeit / Signifikanzniveau
Angenommen wir finden tatsächlich 10 beschädigte Knöpfe (oder mehr) in der Stichprobe und lehnen somit H0 ab.
ABER: Wir könnten uns auch irren und die Behauptung zu Unrecht ablehnen!
Wenn auch die WS gering ist, so kann es doch vorkommen, dass wir 10 schadhafte Knöpfe zählen!
Wie groß ist denn nun diese Irrtumswahrscheinlichkeit ???
Nun, wir zählen einfach die Einzelwahrscheinlichkeiten für 10, 11, 12 usw. schadhafter Knöpfe zusammen, berechnen also α = P(X≥10).
Wozu braucht man die Irrtumswahrscheinlichkeit α?
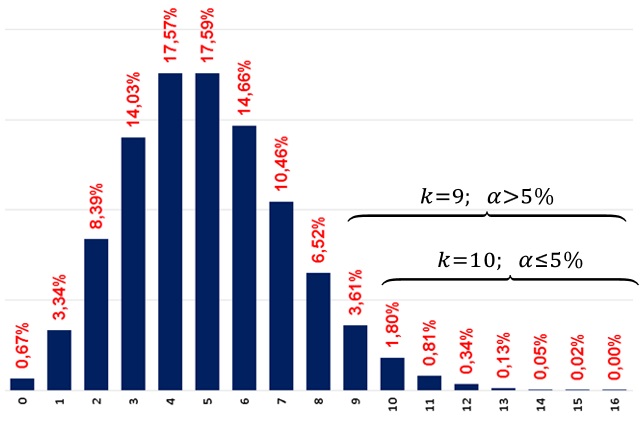
Mathematisch lautet die Aufgabe also: Finde ein „erstes” k, so dass P(X≥k) ≤ α gilt.
Hier haben wir k=10, siehe Abbildung oben.
Rechtsseitiger bzw. linksseitiger Test
In unserem Beispiel liegt der Ablehnungsbereich am rechten Ende der Wahrscheinlichkeitsverteilung. Daher nennt man diese Art von Test einen rechtsseitigen Test.
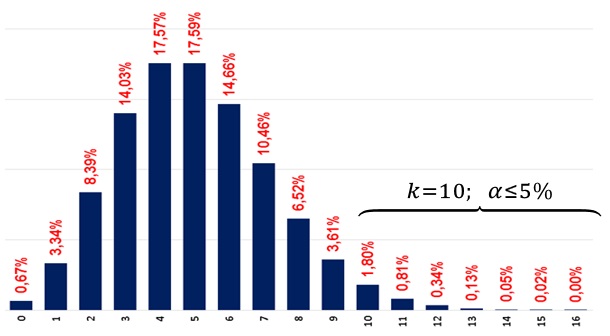
In anderen Aufgabentypen liegt der Ablehnungsbereich am linken Ende. Dies ist dann ein linksseitiger Test.
Bei einem rechtsseitigen Test müssen wir ein k finden, so dass P(X≥k) ≤ α ist, bei einem linksseitigen Test suchen wir hingegen ein k, so dass P(X≤k) ≤ α ist.
Signifikanzniveau
Die Irrtumswsahrscheinlichkeit α nennt man auch das Signifikanzniveau.
Wenn wir also ein „falsches” k wählen (in unserem Fall eine zu geringe Anzahl an beschädigten Knöpfen), dann überschreiten wir das Signifikanzniveau, d.h. es wird immer wahrscheinlicher, dass wir H0 zu unrecht ablehnen.
Wählen wir k=9 (beschädigte Knöpfe), so überschreiten wir das Signifikanzniveau.
Für k=10 liegen wir unterhalb des Signifikanzniveaus, also unterhalb der Irrtumswahrscheinlichkeit.
Entscheidungsregel
Das Signifikanzniveau liefert uns somit eine Entscheidungsregel, d.h. eine Anzahl k (an schadhaften Knöpfen) ab der wir H0 „guten Gewissens” ablehnen können.
In unserem Beispiel lautet die Entscheidungsregel:
Wenn wir in einer Stichprobe von 1000 Knöpfen 10 oder mehr schadhafte Knöpfe finden, dann lehnen wir die Behauptung der Knopfloch AG, nämlich, dass die Ausschussrate unter 0,5% liegt, ab!
Wir glauben dann vielmehr, dass die Ausschussrate größer ist, was man auch die Gegenhypothese nennt.
Mögliche Aufgabenstellungen bei Hypothesentests
Gegeben sei eine Stichprobe vom Umfang n. Die Zufallsvariable X gibt die Anzahl an Treffern an.
X sei binomialverteilt und die Trefferwahrscheinlichkeit sei p. Manchmal ist eine Irrtumswahrscheinlichkeit α gegeben.
Je nach Aufgabentyp kann nun gesucht sein …
1. Ein Ablehnungs- oder Annahmebereich
2. Eine Entscheidungsregel
3. Das Signifikanzniveau (falls nicht gegeben)
| Downloads |
PowerPoint